GW特別指令！！
2024.04.25｜お知らせ
2021.03.19 ｜ お知らせ
目で見る数学？！
生田の個別指導学習塾【英才個別学院 生田校】
こんにちは！英才個別学院 生田校 講師の小城です！
皆さん、数学は好きですか？
私は現在理工学部数学科に所属しており、数学が大好きです！
特に、記号や文字で表されたものがグラフやコンピュータ上、自分の頭のなかでイメージすることができたとき、「数学って面白いなあ」と強く思います。
今日は、私が大学で習う数学のなかで特に面白いと思ったことについて述べたいと思います。
数学には同値関係という考え方があります。
そして、同値関係によって、あるものの集まりを分割すると面白いことがおこります。
定義まで詳しく説明すると大分長くなるのでおおまかに説明すると、
あるものの集まり（集合）のなかで同値関係が成り立っているとき、その同値関係は集合を同値類に分類します。
何をいっているのかわからないと思いますが、もっと簡単にいうとすれば、
（同値関係が成り立つという）条件さえ満たせば、考えたいものの集まりを同一視することができる、ということです。
ここまで読んで全く理解ができていなくても大丈夫です！
なぜなら、皆さんが知らないうちにこの考え方を使っているからです。
例えば、分数もこの同値関係で同一視しています。
１/３も２/6も100/300も同じ値として同一視してますよね
つまり、約分や通分をして同じになるものは同値、としているわけです。
この同値関係を数直線やグラフ上で考えると面白いことがおこります。
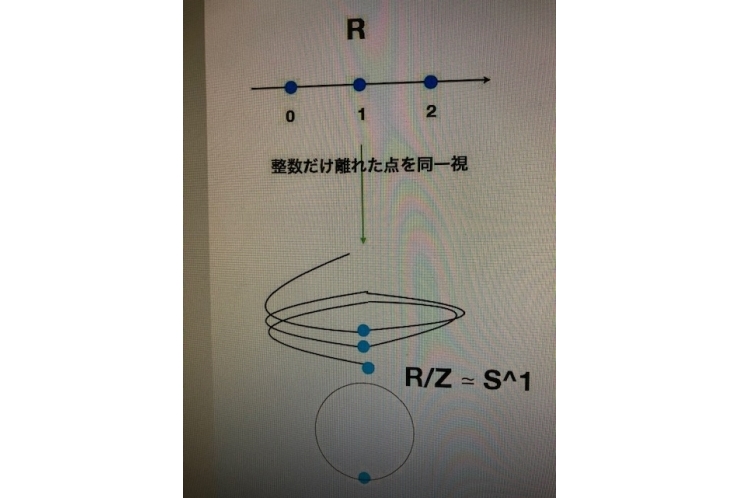
画像のように
無限に続く数直線（実数）のうち、1だけ離れた点（整数）を同一視します。
すると、0，1，2，・・・は同じ点として考えることができ、
直線をばねのように曲げて円環上に重ね合わせたものとして考えることができます。
実は、実数を整数によって同一視すると円周になるんです！
今まで数字の集まりとしか認識していなかった実数が、同値関係をつかって同一視されることにより円周として目で見ることができるようになるなんて面白いですよね。
ここでは数直線（実数）を整数で同一視することを紹介しました。
では、座標平面を整数で同一視すると、どのようなものがあらわれるでしょうか。
分かった時にはきっと数学が好きになっていると思います。
ご興味のある方、お問い合わせは↓こちらから！
ご興味のある方、お電話でのお問い合わせはこちらから！
TEL：044-933-3311
無料体験のお申込みはリンク先の最下段から↓！
https://www.eisai.org/free_trial/
資料請求はこちらから↓！
https://www.eisai.org/request/
英才個別学院 生田校
住所：川崎市 多摩区 生田 7-6-11 エスト生田１Ｆ
小田急線生田駅より 線路沿いに徒歩１分！
ＴＥＬ：044-933-3311
MAIL：ikuta@eisai.org
営業時間 月～金 １４：００～２０：００
土 １４：００～２０：００
